What are Sampling Types Errors and Strategies in Nursing Research a Comprehensive Guide for Educators and Students. Nursing research requires careful sampling to select representative samples from a target population.
The Comprehensive Guide for Educators and Students Sampling Types Errors and Strategies in Nursing Research
This involves using probability sampling (such as simple or stratified random sampling) for generalization, or nonprobability sampling (such as convenience or purposive sampling) to obtain more in-depth information. It is essential to minimize sampling errors, resulting from sample deviations from the population, and non-sampling errors, such as nonresponse or bias.
Strategies include using an updated sampling frame, increasing sample size, employing methods appropriate for quantitative or qualitative studies, and developing clear protocols to reduce bias and error, thereby ensuring the validity and reliability of the research.
Why Sampling Matters in Nursing Research
The quality of a piece of research not only stands or falls by the appropriateness of methodology and instrumentation but also by the suitability of the sampling strategy that has been adopted (see also Morrison, 1993:112–17). Questions of sampling arise directly out of the issue of defining the population on which the research will focus. Researchers must take sampling decisions early in the overall planning of a piece of research. Factors such as expense, time and accessibility frequently prevent researchers from gaining information from the whole population.
Therefore they often need to be able to obtain data from a smaller group or subset of the total population in such a way that the knowledge gained is representative of the total population (however defined) under study. This smaller group or subset is the sample. Experienced re searchers start with the total population and work down to the sample. By contrast, less experienced researchers often work from the bot tom up; that is, they determine the minimum number of respondents needed to conduct the research (Bailey, 1978).
However, unless they identify the total population in advance, it is virtually impossible for them to assess how representative the sample is that they have drawn. Suppose that a class teacher has been released from her teaching commitments for one month in order to conduct some research into the abilities of 13-year-old students to undertake a set of science experiments and that the research is to draw on three secondary schools which contain 300 such students each, a total of 900 students, and that the method that the teacher has been asked to use for data collection is a semi-structured interview.
Because of the time available to the teacher it would be impossible for her to interview all 900 students (the total population being all the cases). Therefore she has to be selective and to interview fewer than all 900 students. How will she decide that selection; how will she select which students to interview? If she were to interview 200 of the students, would that be too many? If she were to interview just twenty of the students would that be too few? If she were to interview just the males or just the females, would that give her a fair picture?
If she were to interview just those students whom the science teachers had decided were ‘good at science’, would that yield a true picture of the total population of 900 students? Perhaps it would be better for her to interview those students who were experiencing difficulty in science and who did not enjoy science, as well as those who were ‘good at science’. So she turns up on the days of the interviews only to find that those students who do not enjoy science have decided to absent themselves from the science lesson.
Understanding the Four Pillars of Sampling Decisions
How can she reach those students? Decisions and problems such as these face researchers in deciding the sampling strategy to be used. Judgements have to be made about four key factors in sampling:
1 the sample size
2 the representativeness and parameters of the sample
3 accesses to the sample
4 the sampling strategy to be used
The decisions here will determine the sampling strategy to be used.
Determining Sample Size: Art Meets Science
A question that often plagues novice researchers is just how large their samples for the research should be. There is no clear-cut answer, for the correct sample size depends on the purpose of the study and the nature of the population under scrutiny.
Sample Size Guidelines by Research Type
However it is possible to give some advice on this matter. Thus, a sample size of thirty is held by many to be the mini mum number of cases if researchers plan to use some form of statistical analysis on their data. Of more import to researchers is the need to think out in advance of any data collection the sorts of relationships that they wish to explore within subgroups of their eventual sample. The number of variables researchers set out to control in their analysis and the types of statistical tests that they wish to make must inform their decisions about sample size prior to the actual research undertaking.
As well as the requirement of a minimum number of cases in order to examine relationships between subgroups, researchers must obtain the minimum sample size that will accurately represent the population being targeted. With respect to size, will a large one guarantee representativeness? Surely not! In the example above the researcher could have interviewed a total sample of 450 females and still not have represented the male population. Will small size guarantee representativeness?
Again, surely not! The latter falls into the trap of saying that 50 per cent of those who expressed an opinion said that they enjoyed science, when the 50 per cent was only one student, a researcher having interviewed only two students in all. Furthermore, too large a sample might become unwieldy and too small a sample might be unrepresentative (e.g. in the first example, the researcher might have wished to interview 450 students but this would have been unworkable in practice or the researcher might have interviewed only ten students, which would have been unrepresentative of the total population of 900 students).
Where simple random sampling is used, the sample size needed to reflect the population value of a particular variable depends both on the size of the population and the amount of heterogeneity in the population (Bailey, 1978). Generally, for populations of equal heterogeneity, the larger the population, the larger the sample that must be drawn.
For populations of equal size, the greater the heterogeneity on a particular variable, the larger the sample that is needed. To the extent that a sample fails to represent accurately the population involved, there is sampling error, discussed below. Sample size is also determined to some extent by the style of the research. For example, a survey style usually requires a large sample, particularly if inferential statistics are to be calculated.
Qualitative vs Quantitative Considerations
In an ethnographic or qualitative style of research it is more likely that the sample size will be small. Sample size might also be constrained by cost— in terms of time, money, stress, administrative support, the number of researchers, and resources. Borg and Gall (1979:194–5) suggest that correlational research requires a sample size of no fewer than thirty cases, that causal-comparative and experimental methodologies require a sample size of no fewer than fifteen cases, and that survey research should have no fewer than 100 cases in each major subgroup and twenty to fifty in each minor subgroup.
They advise (ibid.: 186) that sample size has to begin with an estimation of the smallest number of cases in the smallest subgroup of the sample, and ‘work up’ from that, rather than vice versa. So, for example, if 5 per cent of the sample must be teenage boys, and this sub-sample must be thirty cases (e.g. for correlational research), then the total sample will be 30÷0.05=600; if 15 per cent of the sample must be teenage girls and the sub-sample must be forty-five cases, then the total sample must be 45÷0.15=300 cases.
The size of a probability (random) sample can be determined in two ways, either by the re searcher exercising prudence and ensuring that the sample represents the wider features of the population with the minimum number of cases or by using a table which, from a mathematical formula, indicates the appropriate size of a random sample for a given number of the wider population (Morrison, 1993:117).
Mathematical Approaches to Sample Size Calculation
One such ex ample is provided by Krejcie and Morgan (1970). This suggests that if the researcher were devising a sample from a wider population of thirty or fewer (e.g. a class of students or a group of young children in a class) then she/he would be well advised to include the whole of the wider population as the sample.
The key point to note about the sample size is that the smaller the number of cases there are in the wider, whole population, the larger the proportion of that population must be which appears in the sample; the converse of this is true: the larger the number of cases there are in the wider, whole population, the smaller the proportion of that population can be which appears in the sample. Krejcie and Morgan (1970) note that ‘as the population increases the sample size increases at a diminishing rate and remains constant at slightly more than 380 cases’ (ibid.: 610).
Hence, for example, a piece of research involving all the children in a small primary or elementary school (up to 100 students in all) might re quire between 80 per cent and 100 per cent of the school to be included in the sample, whilst a large secondary school of 1,200 students might require a sample of 25 per cent of the school in order to achieve randomness. As a rough guide in a random sample, the larger the sample, the greater is its chance of being representative.
Understanding and Managing Sampling Error
Another approach to determining sample size for a probability sample is in relation to the confidence level and sampling error. For example, with confidence levels of 95 per cent and 99 per cent and sampling errors of 5 per cent and 1 per cent respectively, the following can be set as sample sizes.
As with the table from Krejcie and Morgan earlier, we can see that the size of the sample reduces at an increasing rate as the population size increases; generally (but, clearly, not always) the larger the population, the smaller the proportion of the probability sample can be. Borg and Gall (1979:195) suggest that, as a general rule, sample sizes should be large where:
- there are many variables
- only small differences or small relationships are expected or predicted
- the sample will be broken down into sub groups
- the sample is heterogeneous in terms of the variables under study
- reliable measures of the dependent variable are unavailable.
Oppenheim (1992:44) adds to this the view that the nature of the scales to be used also exerts an influence on the sample size. For nominal data the sample sizes may well have to be larger than for interval and ratio data (i.e. a variant of the issue of the number of subgroups to be ad dressed, the greater the number of subgroups or possible categories, the larger the sample will have to be).
Borg and Gall (ibid.) set out a formula-driven approach to determining sample size (see also Moser and Kalton, 1977; Ross and Rust, 1997:427–38), and they also suggest using correlational tables for correlational studies—available in most texts on statistics—‘in reverse’ as it were, to determine sample size (p. 201), i.e. looking at the significance levels of correlation co-efficient and then reading off the sample sizes usually required to demonstrate that level of significance.
For example, a correlational significance level of 0.01 would require a sample size of 10 if the estimated co-efficient of correlation is 0.65, or a sample size of 20 if the estimated correlation co-efficient is 0.45, and a sample size of 100 if the estimated correlation co-efficient is 0.20. Again, an inverse proportion can be seen—the larger the sample size, the smaller the estimated correlation co-efficient can be to be deemed significant. With both qualitative and quantitative data, the essential requirement is that the sample is representative of the population from which it is drawn. In a dissertation concerned with a life history (i.e. n=1), the sample is the population!
Qualitative data
In a qualitative study of thirty highly able girls of similar socio-economic background following an A-level Biology course, a sample of five or six may suffice the researcher who is prepared to obtain additional corroborative data by way of validation. Where there is heterogeneity in the population, then a larger sample must be selected on some basis that respects that heterogeneity. Thus, from a staff of sixty secondary school teachers differentiated by gender, age, subject specialism, management or classroom responsibility, etc., it would be insufficient to construct a sample consisting of ten female classroom teachers of Arts and Humanities subjects.
Quantitative data
For quantitative data, a precise sample number can be calculated according to the level of accuracy and the level of probability that the re searcher requires in her work. She can then report in her study the rationale and the basis of her research decision (Blalock, 1979). By way of example, suppose a teacher/re searcher wishes to sample opinions among 1,000 secondary school students. She intends to use a 10-point scale ranging from 1=totally unsatisfactory to 10=absolutely fabulous.
She already has data from her own class of thirty students and suspects that the responses of other students will be broadly similar. Her own students rated the activity (an extra-curricular event) as follows: mean score=7.27; standard deviation=1.98. In other words, her students were pretty much ‘bunched’ about a warm, positive appraisal on the 10-point scale. How many of the 1,000 students does she need to sample in order to gain an accurate (i.e. reliable) assessment of what the whole school (n=1,000) thinks of the extra-curricular event? It all depends on what degree of accuracy and what level of probability she is willing to accept. A simple calculation from a formula by Blalock (1979:215–18) shows that:
- if she is happy to be within + or – 0.5 of a scale point and accurate 19 times out of 20, then she requires a sample of 60 out of the 1,000;
- if she is happy to be within + or – 0.5 of a scale point and accurate 99 times out of 100, then she requires a sample of 104 out of the 1,000;
- if she is happy to be within + or – 0.5 of a scale point and accurate 999 times out of 1,000, then she requires a sample of 170 out of the 1,000;
- if she is a perfectionist and wishes to be within + or – 0.25 of a scale point and accurate 999 times out of 1,000, then she requires a sample of 679 out of the 1,000.
Determining the size of the sample will also have to take account of attrition and respondent mortality, i.e. that some participants will leave the research or fail to return questionnaires. Hence it is advisable to overestimate rather than to underestimate the size of the sample required. It is clear that sample size is a matter of judgements as well as mathematical precision; even formula-driven approaches make it clear that there are elements of prediction, standard error and human judgements involved in determining sample size.
Understanding and Managing Sampling Error
If many samples are taken from the same population, it is unlikely that they will all have characteristics identical with each other or with the population; their means will be different. In brief, there will be sampling error (see Cohen and Holliday, 1979; 1996).
What is Sampling Error?
Sampling error is often taken to be the difference between the sample mean and the population mean. Sampling error is not necessarily the result of mistakes made in sampling procedures. Rather, variations may occur due to the chance selection of different individuals. For ex ample, if we take a large number of samples from the population and measure the mean value of each sample, then the sample means will not be identical. Some will be relatively high, some relatively low, and many will cluster around an average or mean value of the samples. We show this diagrammatically.
Central Limit Theorem in Practice
Why should this occur? We can explain the phenomenon by reference to the Central Limit Theorem which is derived from the laws of probability. This states that if random large samples of equal size are repeatedly drawn from any population, then the mean of those samples will be approximately normally distributed. The distribution of sample means approaches the normal distribution as the size of the sample increases, regardless of the shape—normal or otherwise—of the parent population (Hopkins, Hopkins and Glass, 1996:159, 388).
Moreover, the average or mean of the sample means will be approximately the same as the population mean. The authors demonstrate this (pp. 159 62) by reporting the use of computer simulation to examine the sampling distribution of means when computed 10,000 times. Rose and Sullivan (1993:144) remind us that 95 per cent of all sample means fall between plus or minus 1.96 standard errors of the sample and population means, i.e. that we have a 95 per cent chance of having a single sample mean within these limits, that the sample mean will fall within the limits of the population mean.
By drawing a large number of samples of equal size from a population, we create a sampling distribution. We can calculate the error involved in such sampling. The standard deviation of the theoretical distribution of sample means is a measure of sampling error and is called the standard error of the mean (SEM ).
Thus,
where
SDS = the standard deviation of the sample and
N = the number in the sample. Strictly speaking,
the formula for the standard error of the mean is:
where
SD pop =the standard deviation of the population.
However, as we are usually unable to ascertain the SD of the total population, the standard deviation of the sample is used instead. The standard error of the mean provides the best estimate of the sampling error. Clearly, the sampling error depends on the variability (i.e. the heterogeneity) in the population as measured by SDpop as well as the sample size (N) (Rose and Sullivan, 1993:143). The smaller the SD pop the smaller the sampling error; the larger the N, the smaller the sampling error. Where the SD pop is very large, then N needs to be very large to counteract it.
Where SD pop is very small, then N, too, can be small and still give a reasonably small sampling error. As the sample size increases the sampling error decreases. Hopkins, Hopkins and Glass (1996:159) suggest that, unless there are some very unusual distributions, samples of twenty-five or greater usually yield a normal sampling distribution of the mean. For further analysis of steps that can be taken to cope with the estimation of sampling in surveys we refer the reader to Ross and Wilson (1997).
Standard Error Calculations
We said earlier that one answer to ‘How big a sample must I obtain?’ is ‘How accurate do I want my results to be?’ This is well illustrated in the following example: A school principal finds that the 25 students she talks to at random are reasonably in favor of a proposed change in the lunch break hours, 66 per cent being in favor and 34 per cent being against. How can she be sure that these proportions are truly representative of the whole school of 1,000 students? A simple calculation of the standard error of pro portions provides the principal with her answer.
where
P =the percentage in favor
Q=100 per cent–P
N =the sample size
The formula assumes that each sample is drawn on a simple random basis. A small correction factor called the finite population correction (fpc) is generally applied as follows:
In our example above, of the school principal’s interest in lunch break hours, with a sample of 25, the SE=9.4. In other words, the favorable vote can vary between 56.6 per cent and 75.4 per cent; likewise, the unfavorable vote can vary between 43.4 per cent and 24.6 per cent. Clearly, a voting possibility ranging from 56.6 per cent in favour to 43.4 per cent against is less decisive than 66 per cent as opposed to 34 per cent.
Should the school principal enlarge her sample to include 100 students, then the SE be comes 4.5 and the variation in the range is reduced to 61.5 per cent–70.5 per cent in favour and 38.5 per cent–29.5 per cent against. Sampling the whole school’s opinion (n=1,000) reduces the SE to 1.5 and the ranges to 64.5 per cent–67.5 per cent in favour and 35.5 per cent 32.5 per cent against. It is easy to see why political opinion surveys are often based upon sample sizes of 1,000 to 1,500 (Gardner, 1978).
Ensuring Sample Representativeness
The researcher will need to consider the extent to which it is important that the sample in fact represents the whole population in question (in the example above, the 1,000 students), if it is to be a valid sample. The researcher will need to be clear what it is that is being represented, i.e. to set the parameter characteristics of the wider population—the sampling frame—clearly and correctly.
There is a popular example of how poor sampling may be unrepresentative and unhelpful for a researcher. A national newspaper reports that one person in every two suffers from backache; this headline stirs alarm in every doctor’s surgery throughout the land. However, the newspaper fails to make clear the parameters of the study which gave rise to the head line. It turns out that the research took place:
(a) in a damp part of the country where the incidence of backache might be expected to be higher than elsewhere
(b) in a part of the country which contained a disproportionate number of elderly people, again who might be expected to have more backaches than a younger population
(c) in an area of heavy industry where the working population might be expected to have more backache than in an area of lighter industry or service industries
(d) by using two doctors’ records only, overlooking the fact that many backache sufferers did not go to those doctors’ surgeries because the two doctors concerned were known to regard backache sufferers with suspicion—as shirkers from work.
These four variables—climate, age group, occupation and reported incidence—were seen to exert a disproportionate effect on the study, i.e. if the study were to have been carried out in an area where the climate, age group, occupation and reporting were to have been different, then the results might have been different. The newspaper report sensationally generalized beyond the parameters of the data, thereby overlooking the limited representativeness of the study.
Navigating Access Challenges
Researchers will need to ensure not only that access is permitted, but is, in fact, practicable. For example, if a researcher was to conduct research into truancy and unauthorized absence from school, and she decided to interview a sample of truants, the research might never commence as the truants, by definition, would not be present! Similarly access to sensitive areas might not only be difficult but problematical both legally and administratively, for example, access to child abuse victims, child abusers, dis affected students, drug addicts, school refusers, bullies and victims of bullying.
In some sensitive areas access to a sample might be denied by the potential sample participants themselves, for example an AIDS counsellor might be so seriously distressed by her work that she simply cannot face discussing with a researcher its traumatic subject matter; it is distressing enough to do the job without living through it again with a researcher. Access might also be denied by the potential sample participants themselves for very practical reasons, for example a doctor or a teacher simply might not have the time to spend with the researcher.
Further, access might be denied by people who have something to protect, for example, a person who has made an important discovery or a new invention and who does not wish to disclose the secret of her success; the trade in intellectual property has rendered this a live issue for many researchers. There are very many reasons which might prevent access to the sample, and researchers cannot afford to neglect this potential source of difficulty in planning research. Not only might access be problematic, but its corollary—release of information—might also be problematic.
For example, a researcher might gain access to a wealth of sensitive information and appropriate people, but there might be a restriction on the release of the data collection: in the field of education in the UK, reports have been known to be suppressed, delayed or ‘doctored’. It is not always enough to be able to ‘get to’ the sample, the problem might be to ‘get the information out’ to the wider public, particularly if it could be critical of powerful people.
Sampling Strategy To Be Used
There are two main methods of sampling (Cohen and Holliday, 1979, 1982, 1996; Schofield, 1996). The researcher must decide whether to opt for a probability (also known as a random sample) or a non-probability sample (also known as a purposive sample). The difference between them is this: in a probability sample the chances of members of the wider population being selected for the sample are known, whereas in a non-probability sample the chances of members of the wider population being selected for the sample are unknown.
In the former (probability sample) every member of the wider population has an equal chance of being included in the sample; inclusion or exclusion from the sample is a matter of chance and nothing else. In the latter (non-probability sample) some members of the wider population definitely will be excluded and others definitely included (i.e. every member of the wider population does not have an equal chance of being included in the sample). In this latter type the researcher has deliberately—purposely—selected a particular section of the wider population to include in or exclude from the sample.
Probability Samples
A probability sample, because it draws randomly from the wider population, will be useful if the researcher wishes to be able to make generalizations, because it seeks representativeness of the wider population. This is a form of sampling that is popular in randomized controlled trials. On the other hand, a non-probability sample deliberately avoids representing the wider population; it seeks only to represent a particular group, a particular named section of the wider population, e.g. a class of students, a group of students who are taking a particular examination, a group of teachers.
A probability sample will have less risk of bias than a non-probability sample, whereas, by contrast, a non-probability sample, being unrepresentative of the whole population, may demonstrate skewness or bias. This is not to say that the former is bias-free; there is still likely to be sampling error in a probability sample (discussed below), a feature that has to be acknowledged, for example opinion polls usually declare their error factors, e.g. ± 3 per cent.
Probability Sampling Methods: When You Need Generalizability
There are several types of probability samples: simple random samples; systematic samples; stratified samples; cluster samples; stage samples, and multi-phase samples. They all have a measure of randomness built into them and therefore have a degree of generalizability.
Simple Random Sampling
In simple random sampling, each member of the population under study has an equal chance of being selected and the probability of a member of the population being selected is unaffected by the selection of other members of the population, i.e. each selection is entirely independent of the next. The method involves selecting at random from a list of the population (a sampling frame) the required number of subjects for the sample.
This can be done by drawing names out of a hat until the required number is reached, or by using a table of random numbers set out in matrix form (these are reproduced in many books on quantitative research methods and statistics), and allocating these random numbers to participants or cases (e.g. Hopkins, Hopkins and Glass, 1996:148–9).
Because of probability and chance, the sample should contain subjects with characteristics similar to the population as a whole; some old, some young, some tall, some short, some fit, some unfit, some rich, some poor etc. One problem associated with this particular sampling method is that a complete list of the population is needed and this is not always readily available.
Systematic Sampling
This method is a modified form of simple random sampling. It involves selecting subjects from a population list in a systematic rather than a random fashion. For example, if from a population of, say, 2,000, a sample of 100 is required, then every twentieth person can be selected. The starting point for the selection is chosen at random. One can decide how frequently to make systematic sampling by a simple statistic—the total number of the wider population being represented divided by the sample size required:
Where
f = the frequency interval
N = the total number of the wider population
sn = the required number in the sample.
Let us say that the researcher is working with a school of 1,400 students; by looking at the table of sample size required for a random sample of these 1,400 students we see that 302 students are required to be in the sample. Hence the frequency interval (f) is:
Hence the researcher would pick out every fifth name on the list of cases. Such a process, of course, assumes that the names on the list themselves have been listed in a random order. A list of females and males might list all the females first, before listing all the males; if there were 200 females on the list, the researcher might have reached the desired sample size before reaching that stage of the list which contained males, thereby distorting (skewing) the sample. Another example might be where the researcher decides to select every thirtieth person identified from a list of school students, but it happens that:
1 the school has approximately thirty students in each class;
2 each class is listed from high ability to low ability students;
3 the school listing identifies the students by class.
In this case, although the sample is drawn from each class, it is not fairly representing the whole school population since it is drawing almost exclusively on the higher ability students. This is the issue of periodicity (Calder, 1979). Not only is there the question of the order in which names are listed in systematic sampling, but there is also the issue that this process may violate one of the fundamental premises of probability sampling, namely that every person has an equal chance of being included in the sample.
In the example above where every fifth name is selected, this guarantees that names 1–4, 6–9 etc will not be selected, i.e. that everybody does not have an equal chance to be chosen. The ways to minimize this problem are to ensure that the initial listing is selected randomly and that the starting point for systematic sampling is similarly selected randomly.
Stratified Sampling
Stratified sampling involves dividing the population into homogenous groups, each group containing subjects with similar characteristics. For example, group A might contain males and group B, females. In order to obtain a sample representative of the whole population in terms of sex, a random selection of subjects from group A and group B must be taken. If needed, the exact proportion of males to females in the whole population can be reflected in the sample.
The researcher will have to identify those characteristics of the wider population which must be included in the sample, i.e. to identify the parameters of the wider population. This is the essence of establishing the sampling frame. To organize a stratified random sample is a simple two-stage process.
First, identify those characteristics which appear in the wider population which must also appear in the sample, i.e. divide the wider population into homogeneous and, if possible, discrete groups (strata), for example males and females.
Second, randomly sample within these groups, the size of each group being determined either by the judgements of the researcher or by reference.
The decision on which characteristics to include should strive for simplicity as far as possible, as the more factors there are, not only the more complicated the sampling becomes, but often the larger the sample will have to be to include representatives of all strata of the wider population.
A stratified random sample is, therefore, a useful blend of randomization and categorization, thereby enabling both a quantitative and qualitative piece of research to be undertaken. A quantitative piece of research will be able to use analytical and inferential statistics, whilst a qualitative piece of research will be able to target those groups in institutions or clusters of participants who will be able to be approached to participate in the research.
Cluster Sampling
When the population is large and widely dispersed, gathering a simple random sample poses administrative problems. Suppose we want to survey students’ fitness levels in a particularly large community. It would be completely impractical to select students and spend an inordinate amount of time travelling about in order to test them. By cluster sampling, the researcher can select a specific number of schools and test all the students in those selected schools, i.e. a geographically close cluster is sampled.
Cluster samples are widely used in small scale research. In a cluster sample the parameters of the wider population are often drawn very sharply; a researcher, therefore, would have to comment on the generalizability of the findings. The researcher may also need to stratify within this cluster sample if useful data, i.e. those which are focused and which demonstrate discriminability, are to be acquired.
Stage Sampling
Stage sampling is an extension of cluster sampling. It involves selecting the sample in stages that is, taking samples from samples. Using the large community example in cluster sampling, one type of stage sampling might be to select a number of schools at random, and from within each of these schools, select a number of classes at random, and from within those classes select a number of students. Morrison (1993:121–2) provides an example of how to address stage sampling in practice.
Let us say that a researcher wants to ad minister a questionnaire to all 16-year-olds in each of eleven secondary schools in one region. By contacting the eleven schools she finds that there are 2,000 16-year-olds on roll. Because of questions of confidentiality she is unable to find out the names of all the students so it is impossible to draw their names out of a hat to achieve randomness (and even if she had the names, it would be a mind-numbing activity to write out 2,000 names to draw out of a hat!).
She finds that, for a random sample of the 2,000 students, the sample size is 322 students. How can she proceed? The first stage is to list the eleven schools on a piece of paper and then to put the names of the eleven schools onto a small card and place each card in a hat. She draws out the first name of the school, puts a tally mark by the appropriate school on her list and returns the card to the hat. The process is repeated 321 times, bringing the total to 322. The final totals might appear thus:
School Required no. 1 2 3 4 5 6 7 8 9 10 11
Total of students 15 21 13 52 33 22 38 47 36 22 23 322
For the second stage she then approaches each of the eleven schools and asks them to select randomly the required number of students for each school. Randomness has been maintained in two stages and a large number (2,000) has been rendered manageable. The process at work here is to go from the general to the specific, the wide to the focused, the large to the small.
Multi-Phase Sampling
In stage sampling there is a single unifying purpose throughout the sampling. In the previous example the purpose was to reach a particular group of students from a particular region.
In a multi-phase sample the purposes change at each phase, for example, at phase one the selection of the sample might be based on the criterion of geography (e.g. students living in a particular region); phase two might be based on an economic criterion (e.g. schools whose budgets are administered in markedly different ways); phase three might be based on a political criterion (e.g. schools whose students are drawn from areas with a tradition of support for a particular political party), and so on. What is evident here is that the sample population will change at each phase of the research.
Non-Probability Samples
The selectivity which is built into a non-probability sample derives from the researcher targeting a particular group, in the full knowledge that it does not represent the wider population; it simply represents itself. This is frequently the case in small scale research, for example, as with one or two schools, two or three groups of students, or a particular group of teachers, where no attempt to generalize is desired; this is frequently the case for some ethnographic research, action research or case study research.
Small scale research often uses non-probability samples because, despite the disadvantages that arise from their non-representativeness, they are far less complicated to set up, are consider ably less expensive, and can prove perfectly ad equate where researchers do not intend to generalize their findings beyond the sample in question, or where they are simply piloting a questionnaire as a prelude to the main study.
Just as there are several types of probability sample, so there are several types of non-probability sample: convenience sampling, quota sampling, dimensional sampling, purposive sampling and snowball sampling. Each type of sample seeks only to represent itself or instances of itself in a similar population, rather than attempting to represent the whole, undifferentiated population.
Non-Probability Sampling: When Representation Isn’t The Goal
Convenience Sampling
Convenience sampling—or as it is sometimes called, accidental or opportunity sampling—involves choosing the nearest individuals to serve as respondents and continuing that process until the required sample size has been obtained. Captive audiences such as students or student teachers often serve as respondents based on convenience sampling.
The researcher simply chooses the sample from those to whom she has easy access. As it does not represent any group apart from itself, it does not seek to generalize about the wider population; for a convenience sample that is an irrelevance. The researcher, of course, must take pains to report this point— that the parameters of generalizability in this type of sample are negligible. A convenience sample may be the sampling strategy selected for a case study or a series of case studies.
Quota Sampling
Quota sampling has been described as the non-probability equivalent of stratified sampling (Bai ley, 1978). Like a stratified sample, a quota sample strives to represent significant characteristics (strata) of the wider population; unlike stratified sampling it sets out to represent these in the pro portions in which they can be found in the wider population.
For example, suppose that the wider population (however defined) were composed of 55 per cent females and 45 per cent males, then the sample would have to contain 55 per cent females and 45 per cent males; if the population of a school contained 80 per cent of students up to and including the age of 16, and 20 per cent of students aged 17 and over, then the sample would have to contain 80 per cent of students up to the age of 16 and 20 per cent of students aged 17 and above.
A quota sample, then, seeks to give proportional weighting to selected factors (strata) which reflects their weighting in which they can be found in the wider population. The researcher wishing to devise a quota sample can proceed in three stages:
Stage 1 Identify those characteristics (factors) which appear in the wider population which must also appear in the sample, i.e. divide the wider population into homogeneous and, if possible, discrete groups (strata), for example, males and females, Asian, Chinese and Afro Caribbean.
Stage 2 Identify the proportions in which the selected characteristics appear in the wider population, expressed as a percentage.
Stage 3 Ensure that the percentage proportions of the characteristics selected from the wider population appear in the sample.
Ensuring correct proportions in the sample may be difficult to achieve where the proportions in the wider community are unknown; sometimes a pilot survey might be necessary in order to establish those proportions (and even then sampling error or a poor response rate might render the pilot data problematical). It is straightforward to determine the mini mum number required in a quota sample. Let us say that that the total number of students in a school is 1,700, made up thus:
The proportions being 3:3:6:5, a minimum of 17 students might be required (3+3+6+5) for the sample. Of course this would be a minimum only, and it might be desirable to go higher than this. The price of having too many characteristics (strata) in quota sampling is that the mini mum number in the sample very rapidly could become very large, hence in quota sampling it is advisable to keep the numbers of strata to a minimum. The larger the number of strata the larger the number in the sample will become, usually at a geometric rather than an arithmetic rate of progression.
Purposive Sampling
In purposive sampling, researchers handpick the cases to be included in the sample on the basis of their judgements of their typicality. In this way, they build up a sample that is satisfactory to their specific needs. As its name suggests, the sample has been chosen for a specific purpose, for example:
(a) a group of principals and senior managers of secondary schools is chosen as the research is studying the incidence of stress amongst senior managers
(b) a group of disaffected students has been chosen because they might indicate most distinctly the factors which contribute to students’ disaffection
(c) one class of students has been selected to be tracked throughout a week in or der to report on the curricular and pedagogic diet which is offered to them so that other teachers in the school might compare their own teaching to that reported. Whilst it may satisfy the researcher’s needs to take this type of sample, it does not pretend to represent the wider population; it is deliberately and unashamedly selective and biased.
Dimensional Sampling
One way of reducing the problem of sample size in quota sampling is to opt for dimensional sampling. Dimensional sampling is a further refinement of quota sampling. It involves identifying various factors of interest in a population and obtaining at least one respondent of every combination of those factors. Thus, in a study of race relations, for example, researchers may wish to distinguish first, second and third generation immigrants.
Their sampling plan might take the form of a multi-dimensional table with ‘ethnic group’ across the top and ‘generation’ down the side. A second example might be of a researcher who may be interested in studying disaffected students, girls and secondary aged students and who may find a single disaffected secondary female student, i.e. a respondent who is the bearer of all of the sought characteristics.
Snowball Sampling
In snowball sampling researchers identify a small number of individuals who have the characteristics in which they are interested. These people are then used as informants to identify, or put the researchers in touch with, others who qualify for inclusion and these, in turn, identify yet others—hence the term snowball sampling.
This method is useful for sampling a population where access is difficult, maybe because it is a sensitive topic (e.g. teenage solvent abusers) or where communication networks are undeveloped (e.g. where a researcher wishes to interview stand-in ‘supply’ teachers—teachers who are brought in on an ad hoc basis to cover for absent regular members of a school’s teaching staff—but finds it difficult to acquire a list of these stand-in teachers, or where a researcher wishes to contact curriculum coordinators who have attended a range of in-service courses and built up an informal network of inter school communication).
The task for the re searcher is to establish who are the critical or key informants with whom initial contact must be made. In studies using stratified sampling, applying weights to the data can adjust for the unequal sampling fractions of different strata.
Summary
The message from this post is the same as for many of the others—that every element of the research should not be arbitrary but planned and deliberate, and that, as before, the criterion of planning must be fitness for purpose. The selection of a sampling strategy must be governed by the criterion of suitability. The choice of which strategy to adopt must be mindful of the purposes of the research, the time scales and constraints on the research, the methods of data collection, and the methodology of the research. The sampling chosen must be appropriate for all of these factors if validity is to be served.
Read More:
https://nurseseducator.com/didactic-and-dialectic-teaching-rationale-for-team-based-learning/
https://nurseseducator.com/high-fidelity-simulation-use-in-nursing-education/
First NCLEX Exam Center In Pakistan From Lahore (Mall of Lahore) to the Global Nursing
Categories of Journals: W, X, Y and Z Category Journal In Nursing Education
AI in Healthcare Content Creation: A Double-Edged Sword and Scary
Social Links:
https://www.facebook.com/nurseseducator/
https://www.instagram.com/nurseseducator/
https://www.pinterest.com/NursesEducator/
https://www.linkedin.com/in/nurseseducator/
https://www.researchgate.net/profile/Afza-Lal-Din
https://scholar.google.com/citations?hl=en&user=F0XY9vQAAAAJ



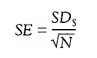
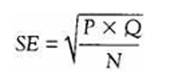

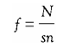



I got what you intend,saved to my bookmarks, very decent site.
Generally I don’t read article on blogs, but I wish to say that this write-up very forced me to try and do so! Your writing style has been amazed me. Thanks, very nice post.
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post…
Thanks a bunch for sharing this with all of us you actually know what you’re talking about! Bookmarked. Please also visit my web site =). We could have a link exchange agreement between us!
I gotta bookmark this site it seems handy very beneficial
What i don’t realize is if truth be told how you’re no longer actually a lot more smartly-liked than you might be right now. You’re very intelligent. You recognize therefore significantly in the case of this topic, made me personally believe it from so many various angles. Its like men and women aren’t fascinated until it is something to do with Girl gaga! Your own stuffs outstanding. At all times maintain it up!
It?¦s actually a nice and useful piece of information. I?¦m glad that you shared this helpful information with us. Please stay us informed like this. Thank you for sharing.
Magnificent goods from you, man. I have understand your stuff previous to and you are just extremely fantastic. I actually like what you’ve acquired here, certainly like what you’re saying and the way in which you say it. You make it entertaining and you still care for to keep it smart. I cant wait to read far more from you. This is really a wonderful web site.