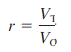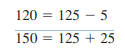Methods of Measurement Reliability II Reliability of Measuring Instruments, split-half technique.
Methods of Measurement Reliability
Four major ways of assessing reliability are test-retest, parallel test, internal consistency, and inter-rater reliability.
Factor Contributor to Reliability Measuring Errors
Methods of Measurement Reliability. In other words, the proportion of true score component in an obtained score varies from one person to the next. Many factors contribute to errors of measurement. The most common are the following:
1. Situational contaminants.
Scores can be affected by the conditions under which they are produced. A participant’s awareness of an observer’s presence (reactivity) is one source of bias. The anonymity of the response situation, the friendliness of researchers, or the location of the data gathering can affect subjects’ responses. Other environmental factors, such as temperature, lighting, and time of day, can represent sources of measurement error.
2. Temporary personal factors.
A person’s score can be influenced by such temporary personal states as fatigue, hunger, anxiety, or mood. In some cases, such factors directly affect the measurement, as when anxiety affects a pulse rate measurement. In other cases, personal factors can alter scores by influencing people’s motivation to cooperate, act naturally, or do their best.
3. Response-set biases.
Relatively enduring characteristics of respondents can interfere with accurate measures. response sets such as social desirability, acquiescence, and extreme responses are potential problems in self-report measures, particularly on psychological scales.
4. Administration variations.
Alterations in the methods of collecting data from one person to the next can result in score variations unrelated to variations in the target attribute. If observers alter their coding categories, if interviewers improvise question wording, if test administrators change the test instructions, or if some physiologic measures are taken before a feeding and others are taken after a feeding, then measurement errors can potentially occur.
5. Instrument clarity.
If the directions for obtaining measures are poorly understood, then scores may be affected by misunderstanding. For example, questions in a self-report instrument may be interpreted differently by different respondents, leading to a distorted measure of the variable. Observers may mis-categorize observations if the classification scheme is unclear.
6.Item sampling.
Errors can be introduced as a result of the sampling of items used in the measure. For example, a nursing student’s score on a 100-item test of nursing knowledge will be influenced somewhat by which 100 questions are included. A person might get 95 questions correct on one test but only 92 right on another similar test.
7. Instrument format.
Technical characteristics of an instrument can influence measurements. Open-ended questions may yield different information than closed-ended ones. Oral responses to a question may be at odds with written responses to the same question. The ordering of questions in an instrument may also influence responses.
Reliability Of Measuring Instruments
Methods of Measurement Reliability. The reliability of a quantitative instrument is a major criterion for assessing its quality and adequacy. An instrument’s reliability is the consistency with which it measures the target attribute. If a scale weighed a person at 120 pounds one minute and 150 pounds the next, we would consider it unreliable. The less variation an instrument produces in repeated measurements, the higher its reliability.
Thus, reliability can be equated with a measure’s stability, consistency, or dependability. Reliability also concerns a measure’s accuracy. An instrument is reliable to the extent that its measures reflect true scores, that is, to the extent that errors of measurement are absent from obtained scores.
Reliable measure maximizes the true score component and minimizes the error component. These two ways of explaining reliability (consistency and accuracy) are not so different as they might appear. Errors of measurement that impinge on an instrument’s accuracy also affect its consistency.
The example of the scale with variable weight readings illustrates this point. Suppose that the true weight of a person is 125 pounds, but that two independent measurements yielded 120 and 150 pounds. In terms of the equation presented in the previous section, we could express the measurements as follows:
The errors of measurement for the two trials (5 and 25, respectively) resulted in scores that are inconsistent and inaccurate. The reliability of an instrument can be assessed in various ways. The method chosen depends on the nature of the instrument and on the aspect of reliability of greatest concern. Three key aspects are stability, internal consistency, and equivalence.
Internal Consistency
Methods of Measurement Reliability. Scales and tests that involve summing items are often evaluated for their internal consistency. Scales designed to measure an attribute ideally are composed of items that measure that attribute and nothing else. On a scale to measure nurses’ empathy, it would be inappropriate to include an item that measures diagnostic competence.
An instrument may be said to be internally consistent or homogeneous to the extent that its items measure the same trait.
Internal consistency reliability is the most widely used reliability approach among nurse researchers. Its popularity reflects the fact that it is economical (it requires only one test administration) and is the best means of assessing an especially important source of measurement error in psychosocial instruments, the sampling of items.
One of the oldest methods for assessing internal consistency is the split-half technique. For this approach, items on a scale are split into two groups and scored independently. Scores on the two half tests then are used to compute a correlation coefficient.
Let us say that the total instrument consists of 20 questions, and so the items must be divided into two groups of 10. Although many splits are possible, the usual procedure is to use odd items versus even items. One half-test, therefore, consists of items 1, 3, 5, 7, 9, 11, 13, 15, 17, and 19, and the even numbered items compose the second half-test. The correlation coefficient for scores on the two half-tests gives an estimate of the scale’s internal consistency. If the odd items are measuring the same attribute as the even items, then the reliability coefficient should be high.
Correlation Coefficient
The correlation coefficient computed on these fictitious data is67. The correlation coefficient computed on split halves tends to underestimate the reliability of the entire scale. Other things being equal, longer scales are more reliable than shorter ones. A correction formula has been developed to give a reliability estimate for the entire test. The equation, known as the Spearman-Brown prophecy formula, is as follows for this situation.
Variability Score
where r the correlation coefficient computed on the split halves r1 the estimated reliability of the entire test Using the formula, the reliability for our hypothetical 20-item measure of self-esteem.
The split-half technique is easy to use but is handicapped by the fact that different reliability estimates can be obtained with different splits. That is, it makes a difference whether one uses an odd even split, a first half second-half split, or some other method of dividing items into two groups. The most widely used method for evaluating internal consistency is coefficient alpha (or Cronbach’s alpha).
Coefficient alpha can be interpreted like other reliability coefficients described here; the normal range of values is between .00 and 1.00, and higher values reflect a higher internal consistency. Coefficient alpha is preferable to the split-half procedure because it gives an estimate of the split-half correlation for all possible ways of dividing the measure into two halves.
It is beyond the scope of this text to explain this method in detail, but more information is available in textbooks on psychometrics (e.g., Cronbach, 1990; Nunnally & Bernstein, 1994).
In summary, indices of homogeneity or internal consistency estimate the extent to which different subparts of an instrument are equivalent in measuring the critical attribute.
The split-half technique has been used to estimate homogeneity, but coefficient alpha is preferable. Neither approach considers fluctuations over time as a source of unreliability.
Read More:
https://nurseseducator.com/didactic-and-dialectic-teaching-rationale-for-team-based-learning/
https://nurseseducator.com/high-fidelity-simulation-use-in-nursing-education/
First NCLEX Exam Center In Pakistan From Lahore (Mall of Lahore) to the Global Nursing
Categories of Journals: W, X, Y and Z Category Journal In Nursing Education
AI in Healthcare Content Creation: A Double-Edged Sword and Scary
Social Links:
https://www.facebook.com/nurseseducator/
https://www.instagram.com/nurseseducator/