Equivalent Interpretation of Reliability Coefficients, Factors Affecting Reliability. Methods of Measurement Reliability, Equivalent, Interpretation of Reliability Coefficients, Factors Affecting Reliability.
Reliability In Nursing Research
Nurse researchers estimate a measure’s reliability by way of the equivalence approach primarily with observational measures. We pointed out that a potential weakness of observational methods is observed error. The accuracy of observer ratings and classifications can be enhanced by careful training, the specification of clearly defined, nonoverlapping categories, and the use of a small number of categories.
Even when such care is taken, researchers should assess the reliability of observational instruments. In this case, “instrument” includes both the category or rating system and the observers making the measurements. Interrater (or interobserver) reliability is estimated by having two or more trained observers watching an event simultaneously, and independently recording data according to the instrument’s instructions.
The data can then be used to compute an index of equivalence or agreement between observers. For certain types of observational data (e.g., ratings), correlation techniques are suitable. That is, a correlation coefficient is computed to demonstrate the strength of the relationship between one observer’s ratings and another’s. Another procedure is to compute reliability as a function of agreements, using the following equation:
Reliability Formula
This simple formula unfortunately tends to overestimate observer agreements. If the behavior under investigation is one that observers code for absence or presence every, say, 10 seconds, the observers will agree 50% of the time by chance alone. Other approaches to estimating interrater reliability may be of interest to advanced students. Techniques such as Cohen’s kappa, analysis of variance, intraclass correlations, and rank-order correlations have been used to assess interobserver reliability.
Interpretation of Reliability Coefficients
Reliability coefficients are important indicators of an instrument’s quality. Unreliable measures do not provide adequate tests of researchers’ hypotheses. If data fail to confirm a prediction, one possibility is that the instruments were unreliable, not necessarily that the expected relationships do not exist.
Knowledge about an instrument’s reliability thus is critical in interpreting research results, especially if research hypotheses are not supported. For group-level comparisons, coefficients in the vicinity of .70 are usually adequate, although coefficients of .80 or greater are highly desirable. By group-level comparisons, we mean that researchers compare scores of groups, such as male versus female or experimental versus control subjects.
If measures are used for making decisions about individuals, then reliability coefficients ideally should be .90 or better. For instance, if a test score was used as a criterion for admission to a graduate nursing program, then the accuracy of the test would be of critical importance to both individual applicants and the school of nursing. Reliability coefficients have a special interpretation that should be briefly explained without elaborating on technical details.
Variability Score
This interpretation relates to the earlier discussion of observed decomposing scores into error components and true components. Suppose we administered a scale that measures hope to 50 cancer patients. It would be expected that the scores would vary from one person to another, that is, some people would be more hopeful than others. Some variability in scores is true variability, reflecting real individual differences in hopefulness; some variability, however, is error.
Thus,
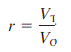
where
VO = observed total variability in scores
VT = true variability
VE = variability owing to random errors
A reliability coefficient is directly associated with this equation. Reliability is the proportion of true variability to the total obtained variability, or
If, for example, the reliability coefficient was .85, then 85% of the variability in obtained scores would represent true individual differences, and 15% of the variability would reflect random, extraneous fluctuations. Looked at in this way, it should be clearer why instruments with reliability lower than .70 are risky to use.
Factors Affecting Reliability
Researchers who develop or adapt instruments for their own use or for use by others must undertake reliability assessments. The availability of computer programs to calculate coefficient alphas has made this task convenient and economical. There are also things that instrument developers should keep in mind during the development process that can enhance reliability.
First, as previously noted, the reliability of composite self-report and observational scales is partly a function of their length (i.e., number of items). To improve reliability, more items tapping the same concept should be added. Items that have no discriminating power (i.e., that elicit similar responses from everyone) should, however, be removed. Scale developers can assess whether items are tapping the same construct and are sufficiently discriminating by doing an item analysis.
In general, items that elicit a 50 50 split (e.g., agree/disagree or correct/incorrect) have the best discriminating power. As a general guideline, if the split is 80/20 or worse, the item should probably be replaced. Another aspect of an item analysis is an inspection of the correlations between individual items and the overall scale score. Item-to-total correlations below .30 are usually considered unacceptably low.
Observational Scales
With observational scales, reliability can usually be improved by greater precision in defining categories, or greater clarity in explaining the underlying dimension for rating scales. The most effective means of enhancing reliability in observational studies, however, is thorough training of observers. The reliability of an instrument is related in part to the heterogeneity of the sample with which it is used.
The more homogeneous the sample (i.e., the more similar their scores), the lower the reliability coefficient will be. This is because instruments are designed to measure differences among those being measured. If the sample is homogeneous, then it is more difficult for the instrument to discriminate reliably among those who possess varying degrees of the attribute being measured.
For example, a depression scale will be less reliable when administered to a homeless sample than when it is used with a general population. Choosing an instrument previously demonstrated to be reliable is no guarantee of its high quality in a new study. An instrument’s reliability is not a fixed entity. The reliability of an instrument is a property not of the instrument but rather of the instrument when administered to a certain sample under certain conditions.
A scale that reliably measures dependence in hospitalized adults may be unreliable with nursing home residents. This means that in selecting an instrument, it is important to know the characteristics of the group with whom it was developed. If the group is similar to the population for a new study, then the reliability estimate provided by the scale developer is probably a reasonably good index of the instrument’s accuracy in the new study.
Finally, reliability estimates vary according to the procedures used to obtain them. A scale’s test-retest reliability is rarely the same value as its internal consistency reliability. In selecting an instrument, researchers need to determine which aspect of reliability (stability, internal consistency, or equivalence) is most relevant.